Diving deep into K-Means

Let's implement K-Means from scratch in PyTorch

What is K-Means?

K-Means is an algorithm that partitions a dataset into K distinct non-overlapping clusters. Every data point is assigned to one and only one cluster. This partitioning is useful for clustering and also for quantization, as we can describe a data point with the index corresponding to the assigned cluster. The algorithm is very simple and aims to minimize the within-cluster variance:

1) Randomly initialize K vectors (centroids) with the same dimensionality as the data. 2) Assign each data point to its closest centroid. 3) Update each centroid as the mean of all data points assigned to it. 4) Iterate 2 and 3 until centroids stop changing.

K-Means doesn’t guarantee convergence to a global minimum, hence it is sensible to the initialization. Some smarter than random initializations have been proposed like K-Means++ and also running the algorithm with different initializations several times and choosing the solution with lowest within-cluster variance.

Another drawback of K-Means is that it doesn’t work well in datasets with non-globular shapes. This is because of euclidean distance, ie. in the moons dataset, the points at the extreme of a moon are further away (in euclidean distance) than the extreme of a moon and the center of the other one.

Why turning it into a PyTorch Layer?

In the context of deep learning, K-Means can be quite handy to discretize data points. For example, in HuBERT discrete targets are created first from audio vectors (MFCCs) and then from internal layers by applying K-Means. For representation learning, it can be useful to promote the formation of clusters. It would be nice to have a K-Means pytorch layer with the following properties:

• It can be plugged into any neural network and perform k-means during the training.
• It can adapt to changing data (online). This is important if we are clustering internal representations from a neural network as they will change during training.
• We don’t want centroids to collapse or be inactive.

Some ideas to try

• Our dataset will change during training, either because we are batching or because the distribution is shifting as the neural network learns. If the centroids change too fast adapting completely to the new dataset, it is likely that they will move too much, and if these centroids are our targets, this can be harmful. One idea is to perform an exponential moving average. This way, the centroids perform gradual updates, moving towards the new locations.
• Another idea, to alleviate the collapse/initialization problem, is to monitor how much the different centroids are being used. If a centroid is inactive, we can replace it. With what? It could be a random point from the dataset, or maybe we can choose the data point that is furthest from any centroid. This idea of choosing a point far from all centroids is also applied in K-Means++ where data points have a higher probability of being chosen as a centroid if they are far from any existing centroid. This way, we are minimizing the risk of duplicating a centroid, and we are maximizing the coverage of the data space.

Some of these ideas are used in random vector quantization to learn codebooks efficiently.

The code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67

class K-MeansOnlineLayer(torch.nn.Module):
    def __init__(self, k, dim, ema_decay=0.8, expire_threshold=2, replacement_strategy='furthest'):
        super().__init__()
        self.k = k
        self.dim = dim
        self.ema_decay = ema_decay
        self.expire_threshold = expire_threshold
        self.replacement_strategy = replacement_strategy
        self._init_parameters()
        
    def _init_parameters(self):
        self.register_buffer('codebook',torch.randn(self.k,self.dim))
        self.register_buffer('cluster_size',torch.zeros((self.k,)))
        self.register_buffer('codebook_sum', self.codebook.clone())

    def euclidean_distance(self, x, y):
        x_norm = torch.tile((x**2).sum(1).view(-1,1),(1,y.shape[0]))
        y_norm = torch.tile((y**2).sum(1).view(-1,1),(1,x.shape[0]))
        xy = torch.mm(x,y.T)
        distances = x_norm + y_norm.T - 2.0*xy
        distances = torch.clamp(distances,0.0,np.inf)
        return distances

    def closest_codebook_entry(self, data):
        #Calculate euclidean distances against all centroids.
        distances = self.euclidean_distance(data, self.codebook)
        #Find the closest centroids for each data point.
        closest_indices = torch.argmin(distances, dim=1)

        return closest_indices, distances

    def update_centroids(self, data, closest_indices):
        # Create a mask for each cluster
        closest_indices_expanded = closest_indices.unsqueeze(1)
        mask = (closest_indices_expanded == torch.arange(self.codebook.shape[0]).unsqueeze(0).to(data.device))

        # For each centroid sum all the points:
        cluster_sums = torch.matmul(mask.T.float(), data)
        # Also count how many points there are in each centroid:
        cluster_counts = mask.sum(dim=0).float()
        # Update the cluster sizes and codebook sums using EMA:
        self.cluster_size.lerp_(cluster_counts, 1 - self.ema_decay)
        self.codebook_sum.lerp_(cluster_sums, 1 - self.ema_decay)
        # Update the centroids by dividing the sum with the size (mean)
        self.codebook = self.codebook_sum / self.cluster_size.unsqueeze(1)
        
    def expire_centroids(self, x, distances):
        # Find unused centroids:
        idxs_replace = self.cluster_size < self.expire_threshold
        num = idxs_replace.sum()
        if num > 0:
            #Replace the unused centroids:
            if self.replacement_strategy == 'furthest':
                replace_points = torch.argsort(torch.min(distances,dim=1).values)[-num:]
            elif self.replacement_strategy == 'random':
                replace_points = torch.randperm(x.shape[0], device = x.device)[:num]
            self.codebook[idxs_replace] = x[replace_points]
            self.cluster_size[idxs_replace] = 1.0
            self.codebook_sum[idxs_replace] = x[replace_points]

    def forward(self, x):
        closest_indices, distances = self.closest_codebook_entry(x)
        if self.training:
            self.update_centroids(x, closest_indices)
            self.expire_centroids(x, distances)
        
        return closest_indices

Checking it works

It seems to be working fine, but… each batch will be a different set of points following a similar distribution to the previous batch. Let’s simulate that situation by sampling at each step a different dataset following the same distribution:

Keeps working! The centroids don’t update too fast thanks to the exponential moving average. Let’s deactivate the EMA and see what happens:

It still works but the centroids change a lot faster, which could get us in trouble? if the assigned cluster is the target of a neural network.

Not only each batch is a different sample of the dataset distribution, but if the dataset comes from an internal representation of a neural network, or if the distribution shifts because data is dynamic (culture changes, different biases are introduced during data collection, etc…), then the distributions of the batches will change. Let’s check the robustness of our model:

It seems to be keeping track of the distribution shifts as the centroids follow closely each gaussian mean, but we have a problem: initialization is leading us to a not so good solution. At the beginning of the animation you can see that 2 of the 3 centroids are close each other. This causes them to distribute the points of one cluster between them. The remaining cluster gets the points belonging to the 2 other gaussians. Ideally we want a centroid for each gaussian but we are getting 2 for one, and one for 2. Can we solve it? Well in theory no, because we can’t guarantee convergence to a global minimum in polynomial time. But we can implement the K-Means++ heuristic in our layer to have a better initialization.

K-Means++

The algorithm for K-Means++ initialization is quite simple:

1) Pick a random data point as the first centroid. 2) Calculate the distances $D(x)$ from each point to the closest centroid. 3) Build a probability distribution so that the higher distance, the higher probability: $P(x’) = \frac{D^2(x’)}{\sum_{x \in X} D^2(x)}$ 4) Sample a data point following $P(x)$ and add it as a new centroid. 5) Repeat steps 2-4 until there are K centroids.

The implementation in PyTorch is quite straight-forward, adding this method to our K-Means layer:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

def K-Means_init(self, x):
    batch_size = x.shape[0]
    centroids = torch.zeros((self.k, self.dim))
    #Initial centroid is a randomly sampled point
    centroids[0] = x[random.randint(0,batch_size-1)]
    #Distance between each point and closest centroid (only one we have):
    min_distances = self.euclidean_distance(x,centroids[0].unsqueeze(0))
    for i in range(self.k-1):
        #Turn distances into probabilities:
        probs = (min_distances**2)/torch.sum(min_distances**2)
        #Sample following the probs:
        centroid_idx = torch.multinomial(probs[:,0],1,replacement=False)
        #Add the new sampled centroid:
        centroids[i+1]=x[centroid_idx]
        #Update the distances:
        distances_new_centroid = self.euclidean_distance(x,centroids[i+1].unsqueeze(0))
        min_distances = torch.minimum(min_distances, distances_new_centroid)
    self.codebook = centroids

Check out our previous initialization vs K-Means++ one:

Random initialization vs K-Means++ initialization.

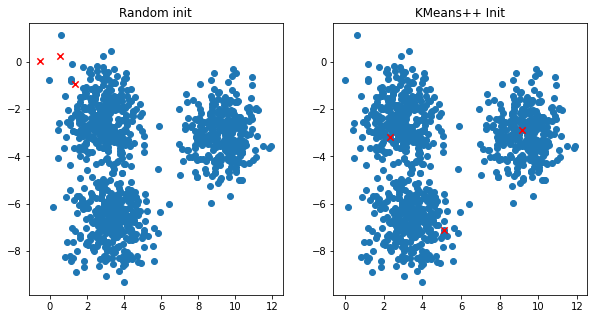
A lot better!

Victory?

Not quite yet! Let’s see what happens if we run the same algorithm many times:

Different runs of K-Means over the same dataset. The red diamonds are the initial centroids determined by K-Means++, the red crosses are the centroids after 50 iterations.

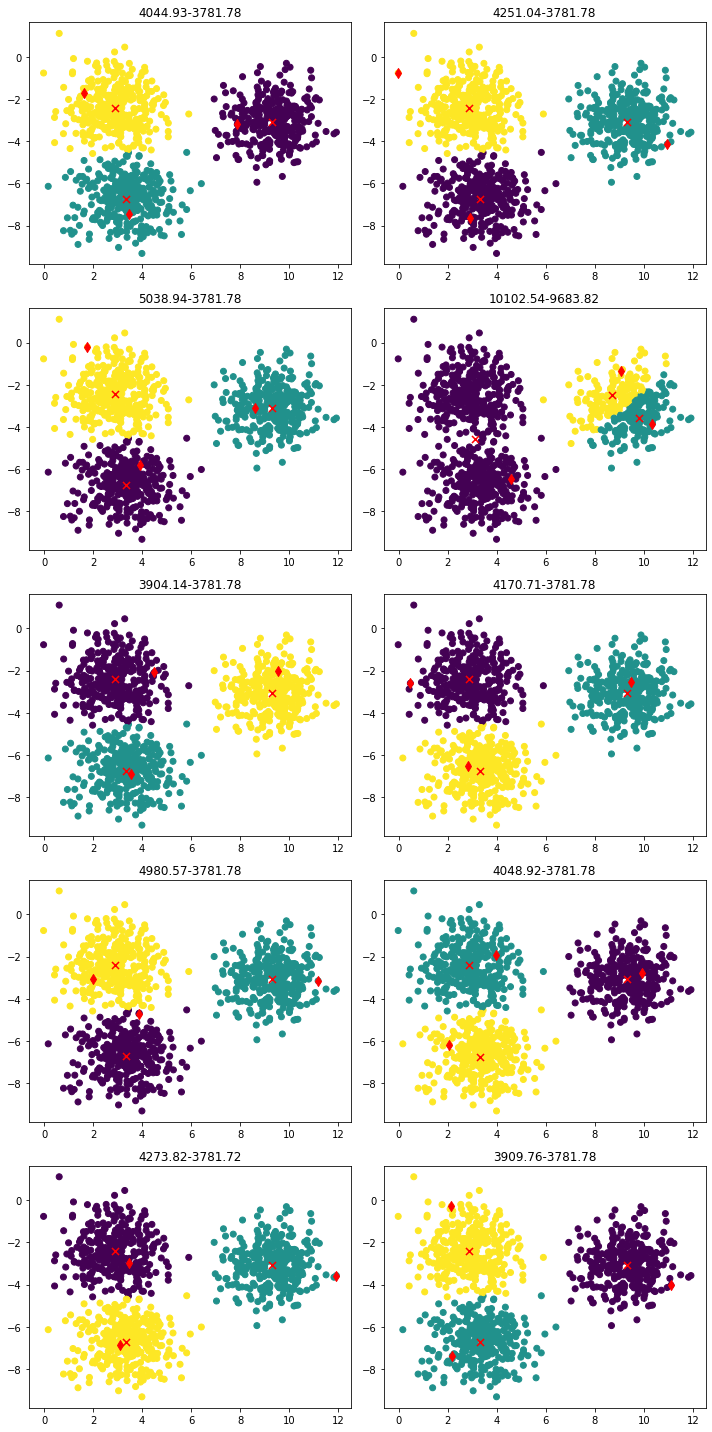
We found the ‘good solution’ 9 times out of 10. Can you spot the bad one?… It’s second row, right column. Well, as I said before, K-Means doesn’t guarantee finding the global minimum. Also, K-Means++ is still a random initialization, so we can sample 2 centroids that are very close each other (this is what happened in the bad solution). What can we do?

Well, let’s just run the algorithm a few times and then choose the best clustering. How can we measure a good clustering?

Within-Class Variance and Reinitialization

K-Means tries to minimize the within-cluster variance (WCV), so let’s run K-Means++ 10 times and measure the resulting WCV. Then, let’s choose the initialization with minimum WCV. The WCV is defined as: \(WCV(X,C) = \sum_{k=1}^K \frac{1}{|C_k|}\sum_{i,i' \in C_k} \sum_{j=1}^D (x_{ij} - x_{i'j})^2\)

where $X$ is our dataset with dimensionality $D$ and $C$ is the cluster assignment so that $C_k$ is the set of indexs corresponding to the cluster $k$. The idea is that we are calculating the pairwise euclidean distance for all the points belonging to a cluster. If the points in each cluster are close each other, then the WCV will be low.

The code for calculating WCV is:

1
2
3
4
5
6
7
8
9
10
11
12

def wcv(self, x):
    closest_indices, distances = self.closest_codebook_entry(x)
    cvsum = 0
    for i in range(self.k):
        ck = closest_indices == i
        ck_cardinal = ck.sum()
        if ck_cardinal > 0:
            cv = torch.sum(self.euclidean_distance(x[ck],x[ck]))/ck_cardinal
        else:
            cv = 0
        cvsum += cv
    return cvsum

The WCV values at initialization and after 50 iterations can be seen in the titles of the previous figure. While the good solutions end up with a WCV of 3781, the bad one ends up with 9683. This hints us that running multiple seeds and choosing the one with less WCV is a good approach to avoid bad solutions. Also notice that WCV always decreases with K-Means algorithm.

You can find the final code and experiments of this article in this colab